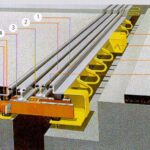
Algemene beschrijving
De voegovergangfamilie “lamellenvoegovergangen”, “meervoudige voegovergangen” of “modulaire voegovergangen” bestaat uit een reeks aan voegovergangconcepten, met als kenmerk de aanwezigheid van meerdere voegspleten door de aanwezigheid van draagbalken (lamellen) met daartussen rubberen afdichtingsprofielen. Het betreft familie 7 uit de RTD1007-1 Meerkeuzematrix voegovergangen (MKM). De concepten onderscheiden zich voornamelijk van elkaar door de manier waarop de lamellen onderling op ongeveer gelijke afstand van elkaar worden gehouden, het zogenaamde stuursysteem.
De verschillende systemen worden verder behandeld in de navolgende paragrafen.
Lamellenvoegen zijn kostbare systemen en worden grotendeels samengesteld uit staal. Nosing joints hebben dus over het algemeen een langere beoogde ontwerplevensduur, doorgaans 30-40 jaar.
Het zal doorgaans gewenst zijn om onderhoud aan en vervanging van voegovergangen synchroon te laten lopen aan de vervanging van de wegverharding. Asfaltdeklagen hebben rijbaanbreed doorgaans een levensduur van 10 tot 20 jaar. Voor lamellenvoegen betekent dit dat deze 3 tot 4 keer de levensduur van een deklaag mee zal gaan en dat benodigd onderhoud (vervangen of reparatie van onderdelen) dus in een gewenste frequentie van 1 x 10-20 jaar uitgevoerd dient te worden.
Toepassingsgebied
Toepassingsgebieden zijn zowel bestaande als nieuwe grote verkeersbruggen, zowel in staal als beton, in alle verkeerscategorieën. Lamellenvoegen kunnen ook worden toegepast in kunstwerken waar enkelvoudige voegovergangen onvoldoende dilatatiecapaciteit hebben als alternatief voor vingervoegen. Daar waar vingervoegen beperkt zijn in zowel dwarsbewegingen als verticale bewegingen bieden lamellenvoegen meestal meer bewegingscapaciteit in deze beide richtingen. Hierop wordt verder ingegaan bij de behandeling van de diverse voegovergangconcepten in de navolgende paragrafen.
De onderdelen van een lamellenvoeg
In onderstaande figuur zijn de diverse onderdelen van een lamellenvoeg weergegeven
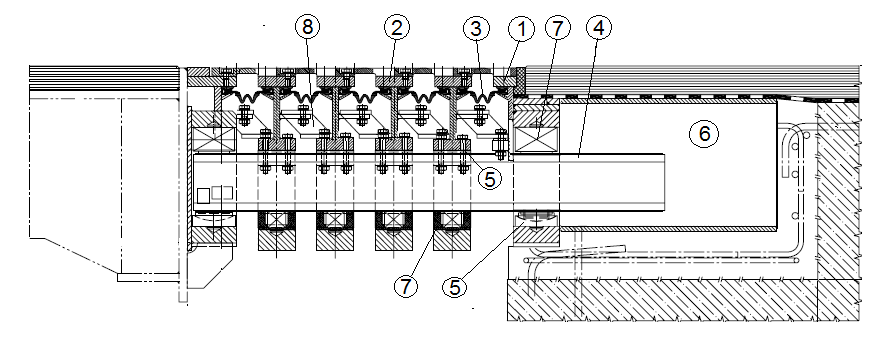
- Randprofiel
In principe gelijk aan het randprofiel van een nieuwbouwmodel 1.2a nosing joint. Het randprofiel zorgt voor de waterdichte aansluiting op de aangrenzende wegverharding en draagt het verkeer - Lamellen:
De lamellen dragen het verkeer tussen de randprofielen - Afdichtingsprofielen
Afdichtingsprofielen zorgen voor de vereeiste waterdichtheid van het systeem. Het water wordt direct tussen de lamellen en het randprofiel gekeerd en afgevoerd naar het laagste punt die aangesloten is op de lijngoot van het brugdek. - Traversebalken of dwarsdragers
Deze balken dragen de lamellen en dragen de verkeersbelasting af naar de aangrenzende constructies. De wijze waarop de lamellen zijn verbonden aan de traversedragers verschilt. In de meeste gevallen zijn de lamellen transleerbaar en roteerbaar ingeklemd opgelegd op de traversebalken (concept 7.2 en 7.3). Bij concept 7.1 is er sprake van een starre verbinding tussen lamel en dwarsdrager waarbij iedere lamel is verbonden met een eigen serie dwarsdragers. Bij concept 7.4 heeft het stuurmechanisme tevens de functie van dwarsdrager en ontbreken afzonderlijke dwarsdragers. - Opleggingen
De traverse balken liggen op opleggingen translatie en rotatie van de traversebalken mogelijk maak en de belasting afvoert naar de traversekasten - Traverse kasten
In de traversekasten zijn de traversebalken opgelegd. De kasten bieden ruimte aan de traversebalken om de dilatatiebewegingen van het kunstwerk te kunnen volgen. - Drukveren
De drukveren zorgen er voor dat de traversebalken als gevolg van het dynamische gedrag niet gaan klapperen. Drukveren zorgen dus dat de traversebalken zonder speling zijn opgesloten in de traversekasten. Drukveren dienen onder een bepaalde voorspanning te staan en dienen de dilatatiebewegingen van de traversebalken niet te verhinderen en zijn daarom voorzien van glijdmateriaal - Stuurmechanisme
Het stuurmechanisme heeft als functie om de lamellen onderling op ongeveer de zelfde afstand te houden en de dilatatiebewegingen dus te verdelen over de ruimte tussen de lamellen.
In de meeste gevallen bestaat het systeem uit elastische stuurveren die in serie met elkaar zijn geschakeld (concept 7.1 en 7.2). Maar er zijn ook systemen waarbij de sturing plaats vind door scharnierwerking (concept 7.3 en 7.4)
Typen
Lamellenvoegen kunnen worden ingedeeld naar type draagsysteem en stuurmechanisme
De volgende draagsystemen kunnen worden onderscheiden :
- Multi-dwarsdrager systeem, waarbij Iedere lamel wordt afzonderlijk ondersteund door eigen dwarsdragers (concept 7.1)
- Enkel dwarsdragersysteem, waarbij alle lamellen worden ondersteund door gemeenschappelijke dwarsdragers (concept 7.2 – 7.4)
Qua stuurmechanisme kunnen de volgende systemen worden onderscheiden
- Lamellen worden gestuurd door stuurveren die in serie geschakeld zijn (concept 7.1 en 7.2)
- Lamellen worden gestuurd door scharnierwerking (concept 7.3 en 7.4)
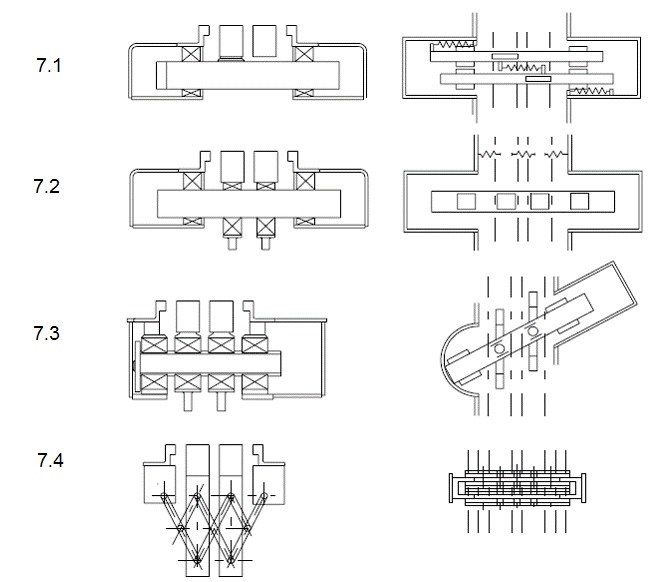
In de Meerkeuzematrix voegovergangen wordt de volgende concepten onderscheiden:
| Concept (type`nr) | Omschrijving | Concept (subtype) | |||
| Nr. | Omschrijving | ||||
| 7.1 | Elke lamel voorzien van aangelaste dwarsdragers, die in stalen doosconstructie (kast) voorgespannen zijn opgelegd | 7.1a1 | zonder geluidreducerende voorziening | ||
| 7.1a2 | met geluidreducerende voorziening | ||||
| 7.2 | Alle lamellen met beugels verbonden op centrale dwarsdragers | 7.2a1 | zonder geluidreducerende voorziening | ||
| 7.2a2 | met geluidreducerende voorziening | ||||
| 7.3 | Alle lamellen met beugels verbonden op centrale zwenkdwarsdragers | 7.3a1 | zonder geluidreducerende voorziening | ||
| 7.3a2 | met geluidreducerende voorziening | ||||
| 7.4 | Alle lamellen verbonden met verkeersdragend scharensysteem | 7.4a1 | zonder geluidreducerende voorziening | ||
| 7.4a2 | met geluidreducerende voorziening | ||||
Dynamische eigenschappen
Algemeen
Lamellenvoegen zijn in veel gevallen al bijna kleine bruggen die belast worden door dynamische belastingen uit het passerende verkeer. De dynamische belasting ontstaan door de ongelijkheden in het wegdek en ook door de dynamische interactie die wordt gedomineerd door de belastingfrequentie en de eigenfrequenties van de voegovergang. Deze eigenfrequenties zijn bijvoorbeeld de grondtonen van de lamellen en de dwarsdragers, maar kunnen in theorie ook de boventonen zijn. Wel moet daarbij rekening worden gehouden met verticale, horizontale en incidenteel ook met torsiefrequenties.
Na het belasten vindt een terugveren plaats dat in het geval van weinig demping, zoals bij staalconstructies, verplaatsingen en interne belastingen geeft, niet die ongeveer gelijk zijn aan de belasting die gepaard gaat met de dynamische toeslag. Daarna dempt de constructie uit. Deze demping vindt plaats door demping in het materiaal, zeer gering in staalconstructies, of systeemdemping waarbij stoorfrequenties een dempende werking hebben of door externe demping door wrijving.
Stootfactoren door ongelijkheden in het wegoppervlak
De ongelijkheden in het wegdekoppervlak veroorzaken verticale en horizontale massakrachten op de passerende assen. In het algemeen veroorzaken deze een verhoging van de reeds aanwezige belasting op de as met een factor tussen 1,1 en 1,3, afhankelijk van de hoogteverschillen, voor verticale en horizontale belastingen bij hoogteverschillen in stijve wegdekken.
Bij typen of onderdelen van lamellen kunnen deze interacties verschillen, afhankelijk van de plaats in de voegovergang.
Stootfactoren door dynamische interactie
Wanneer een onderdeel met een eigenfrequentie gedurende een bepaalde tijd, met een belastingfrequentie, wordt belast dan kan dit worden vertaald in een dynamische vergrotingsfactor. Deze factor is natuurlijk zowel verticaal als horizontaal.
Wanneer een lamel 80 mm breedte heeft en een wielprent een lengte van 300 mm heft, dan is de belastingtijd bepaald door de effectieve contactlengte, in dit geval 380 mm. De snelheid van de voertuigen is bijvoorbeeld 80 km/u, die gelijk is aan 22 m/s. en de effectieve belasting tijd is 0,017 s. die beschouwd kan worden als een belastingfrequentie van 58 Hz. In dit geval zullen de lamel en de onderdelen die de lamel ondersteunen niet door de dynamische interactie worden beïnvloed wanneer hun eigenfrequenties ver van de 58 Hz liggen, dus bijv. minder dan 40 Hz of hoger dan 70 Hz.
Wanneer een dwarsdrager meerdere lamellen ondersteunt, zoals bij het “ single crossbeam type”, dan duurt de verticale belastingtijd van de dwarsdrager natuurlijk veel langer. De belastingtijd van de dwarsdrager wordt dan gevonden door de effectieve belastinglengte, bijv. 4 lamellen van 80 mm breed en 3 spleten van elk 40 mm. De belaste lengte is dan 320 + 120 = 440 mm. Wordt deze vermeerder met twee maal de loopvlaklengte ontstaat een totale belastinglengte van 600 + 440 = 1040 mm. Bij een snelheid van 22 m/s is dit een belastingtijd van 0,047 s. Dit correspondeert met 21 Hz.
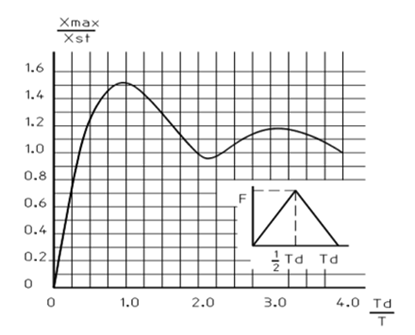
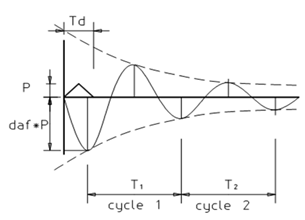
In het figuur is duidelijk te zien dat wanneer de belastingtijd Td samenvalt met de eigen trillingstijd T, de maximale dynamische vergrotingsfactor van ongeveer 1,6 wordt gevonden. Zowel bij een duidelijk groter en een duidelijk kleiner coëfficiënt worden lagere waarden gevonden.
Terugveren
Indien een onderdeel door een dynamische belasting een vervorming in dat onderdeel veroorzaakt hoger dan de statische vervorming, dan zal na ontlasten dit onderdeel terugveren voorbij de stand zonder belasting. Dit fenomeen wordt “upswing” genoemd. Wanneer een constructie weinig demping heeft zal deze waarde ongeveer gelijk zijn aan de toeslag als gevolg van de dynamische belasting. Dus bij een dynamische vergrotingsfactor van 1,3 zal het terugveereffect ongeveer 0,3 zijn. Het volgende figuur laat een belasting met een driehoekige “time-history” zien waar na een belasting een dempende trilling optreedt.
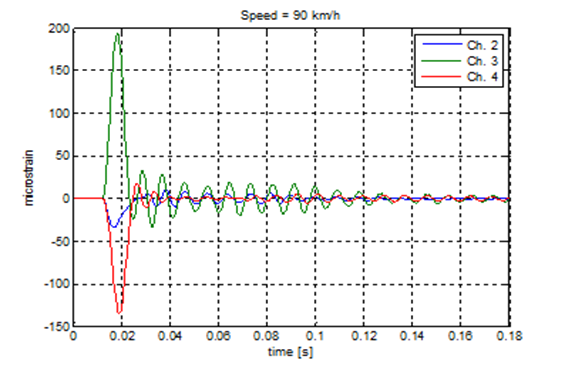
De volgende figuur laat een meting aan de “Maurer balkroostervoeg” zien. Het terugveereffect is zeer beperkt.
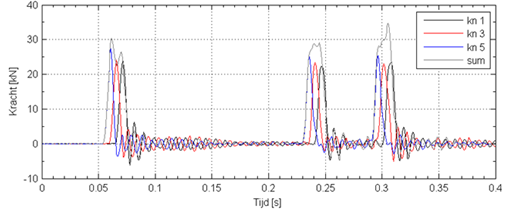
Lamellenmeting:
Demping
Na het beperkte terugveereffect bij de eerste cycle blijkt zowel bij de dwarsdrager als ook bij de lamellen de verdere demping zeer beperkt. Dit zou er op kunnen wijzen dat de eerste cycle wordt gedempt door systeemdemping en externe demping (bijv. wrijving) en de volgende cycli door materiaaldemping.
Nabeschouwing dynamisch gedrag
De dynamische vergroting, het terugveren en de daaropvolgende dempte trilling daat gepaard met spanningsintervallen, die wanneer ze boven de constante amplitude grens voor vermoeiing liggen op den duur kunnen leiden tot scheurvorming. Hoewel hier alleen de verticale bewegingen zijn weergegeven moet bij het ontwerp ook rekening worden gehouden met de horizontale bewegingen en torsie en de interactie tussen deze drie fenomenen.
De locaties die getoetst moeten worden voor vermoeiing zijn in veel gevallen andere dan die bepalend zijn voor de statische sterkte.
Gelaste verbindingen zijn door hun lagere vermoeiingsclassificatie en de spanningsconcentraties die door de detaillering worden opgewekt over het algemeen gevoelig voor vermoeiing. In mindere mate geldt dit voor boutverbindingen.